10 интересных научных парадоксов

Парадокс - это событие, ситуация, действие или бездействие, которое может существовать или уже существует в реальности, но противоречит логическим объяснениям. поломайте голову над предоставленными под катом 10 любопытными парадоксами.
Парадокс Рассела.
Парадокс, который его открыватель, знаменитый британский философ и математик Бертран Рассел называл не иначе, как парадокс брадобрея, строго говоря, можно считать одной из форм парадокса лжеца.
Предположим, проходя мимо парикмахерской, вы увидели на ней рекламное объявление: «Вы бреетесь сами? Если нет, милости просим бриться! Брею всех, кто не бреется сам, и никого другого!». Закономерно задать вопрос: каким образом цирюльник управляется с собственной щетиной, если он бреет только тех, кто не бреется самостоятельно? Если же он сам не бреет собственную бороду, это противоречит его хвастливому утверждению: «Брею всех, кто не бреется сам».
Конечно, легче всего предположить, что недалёкий брадобрей просто не подумал о противоречии, содержащемся в его вывеске и забыть об этой проблеме, но попытаться понять её суть гораздо интереснее, правда для этого придётся ненадолго окунуться в математическую теорию множеств.
Парадокс Рассела выглядит так: «Пусть K — множество всех множеств, которые не содержат себя в качестве собственного элемента. Содержит ли K само себя в качестве собственного элемента? Если да, это опровергает утверждение, что множества в его составе „не содержат себя в качестве собственного элемента“, если же нет, возникает противоречие с тем, что К является множеством всех множеств, не содержащих себя как собственный элемент, а значит K должно содержать все возможные элементы, включая себя».
Проблема возникает из-за того, что Рассел в рассуждениях использовал понятие «множество всех множеств», которое само по себе довольно противоречиво, и руководствовался при этом законами классической логики, которые применимы далеко не во всех случаях (см. пункт шесть).
Открытие парадокса брадобрея спровоцировало жаркие споры в самых разных научных кругах, которые не утихают до сих пор. Для «спасения» теории множеств математики разработали несколько систем аксиом, но доказательств непротиворечивости этих систем нет и, по мнению некоторых учёных, быть не может.

Парадокс ценности.
Феномен, известный также как парадокс алмазов и воды или парадокс Смита (назван в честь Адама Смита — автора классических трудов по экономической теории, который, как считается, первым сформулировал этот парадокс), заключается в том, что хотя вода как ресурс гораздо полезнее кусков кристаллического углерода, называемых нами алмазами, цена последних на международном рынке несоизмеримо выше стоимости воды.
С точки зрения выживания вода действительно нужна человечеству гораздо больше алмазов, однако её запасы, конечно же, больше запасов алмазов, поэтому специалисты говорят, что ничего странного в разнице цен нет — ведь речь идёт о стоимости единицы каждого ресурса, а она во многом определяется таким фактором, как предельная полезность.
При непрерывном акте потребления какого-либо ресурса его предельная полезность и, как следствие, стоимость неизбежно падает — эту закономерность в XIX-м веке открыл прусский экономист Герман Генрих Госсен. Говоря простым языком, если человеку последовательно предложить три стакана воды, первый он выпьет, водой из второго умоется, а третий пойдёт на мытьё пола.
Большая часть человечества не испытывает острой нужды в воде — чтобы получить достаточное её количество, стоит только открыть водопроводный кран, а вот алмазы имеются далеко не у всех, поэтому они столь дороги.

Парадокс убитого дедушки.
Этот парадокс в 1943-м году предложил французский писатель-фантаст Рене Баржавель в своей книге «Неосторожный путешественник» (в оригинале «Le Voyageur Imprudent»).
Предположим, вам удалось изобрести машину времени, и вы отправились на ней в прошлое. Что произойдёт, если вы встретите там своего дедушку и убьёте его до того, как он встретился с вашей бабушкой? Вероятно, не всем понравится этот кровожадный сценарий, поэтому, скажем, вы предотвратите встречу другим путём, например, увезёте его на другой конец света, где он никогда не узнает о её существовании, парадокс от этого не исчезает.
Если встреча не состоится, ваша мать или отец не появится на свет, не сможет зачать вас, а вы соответственно не изобретёте машину времени и не попадёте в прошлое, поэтому дедушка сможет беспрепятственно жениться на бабушке, у них родится один из ваших родителей и так далее — парадокс налицо.
История с убитым в прошлом дедушкой часто приводится учёными как доказательство принципиальной невозможности путешествий во времени, однако некоторые специалисты говорят, что при определённых условиях парадокс вполне разрешим. Например, убив своего дедушку, путешественник во времени создаст альтернативную версию реальности, в которой он никогда не будет рождён.
Кроме того, многие высказывают предположения, что даже попав в прошлое, человек не сможет на него повлиять, так как это приведёт к изменению будущего, частью которого он является. Например, попытка убийства дедушки заведомо обречена на провал — ведь если внук существует, значит, его дед, так или иначе, пережил покушение.

Корабль Тесея.
Название парадоксу дал один из греческих мифов, описывающий подвиги легендарного Тесея, одного из афинских царей. Согласно легенде, афиняне несколько сотен лет хранили корабль, на котором Тесей вернулся в Афины с острова Крит. Конечно, судно постепенно ветшало, и плотники заменяли прогнившие доски на новые, в результате чего в нём не осталось ни кусочка старой древесины. Лучшие умы мира, в числе которых видные философы вроде Томаса Гоббса и Джона Локка веками размышляли над тем, можно ли считать, что именно на этом судне когда-то путешествовал Тесей.
Таким образом, суть парадокса в следующем: если заменить все части объекта на новые, может ли он быть тем же самым объектом? Кроме того, возникает вопрос — если из старых частей собрать точно такой же объект, какой из двух будет «тем самым»? Представители разных философских школ давали прямо противоположные ответы на эти вопросы, но некоторые противоречия в возможных решениях парадокса Тесея до сих пор существуют.
Кстати, если учесть, что клетки нашего организма практически полностью обновляются каждые семь лет, можно ли считать, что в зеркале мы видим того же человека, что и семь лет назад?

Парадокс Галилея.
Открытый Галилео Галилеем феномен демонстрирует противоречивые свойства бесконечных множеств. Краткая формулировка парадокса такова: натуральных чисел столько же, сколько их квадратов, то есть, количество элементов бесконечного множества 1, 2, 3, 4… равно количеству элементов бесконечного множества 1, 4, 9, 16…
На первый взгляд, никакого противоречия здесь нет, однако тот же Галилей в своей работе «Две науки» утверждает: некоторые числа являются точными квадратами (то есть из них можно извлечь целый квадратный корень), а другие нет, поэтому точных квадратов вместе с обычными числами должно быть больше, чем одних точных квадратов. Между тем, ранее в «Науках» встречается постулат о том, что квадратов натуральных чисел столько же, сколько самих натуральных чисел и эти два утверждения прямо противоположны друг другу.
Сам Галилей считал, что парадокс можно решить только применительно к конечным множествам, однако Георг Кантор, один из немецких математиков XIX-го века, разработал свою теорию множеств, согласно которой второй постулат Галилея (об одинаковом количестве элементов) верен и для бесконечных множеств. Для этого Кантор ввёл понятие мощности множества, которые при расчётах для обоих бесконечных множеств совпали.

Парадокс бережливости.
Самая известная формулировка любопытного экономического явления, описанного Уоддилом Кетчингсом и Уильямом Фостером выглядит следующим образом: «Чем больше мы откладываем на чёрный день, тем быстрее он наступит». Чтобы понять суть противоречия, заключённого в этом феномене, немного экономической теории.
Если во время экономического спада большая часть населения начинает экономить свои сбережения, снижается совокупный спрос на товары, что в свою очередь приводит к уменьшению заработка и как следствие — падению общего уровня экономии и сокращению сбережений. Попросту говоря, возникает своего рода замкнутый круг, когда потребители тратят меньше денег, но тем самым ухудшают своё благосостояние.
В некотором роде парадокс бережливости аналогичен проблеме из теории игр под названием дилемма заключённого: действия, которые выгодны каждому участнику ситуации по отдельности, вредны для них в целом.

Парадокс Пиноккио.
Является разновидностью философской проблемы, известной как парадокс лжеца. Этот парадокс прост по форме, но отнюдь не по содержанию. Его можно выразить в трёх словах: «Это утверждение — ложь», или даже в двух — «Я лгу». В варианте с Пиноккио проблема сформулирована так: «Мой нос сейчас растёт».
Думаю, вам понятно противоречие, содержащееся в этом утверждении, но на всякий случай, расставим все точки над ё: если фраза верна, значит, нос действительно растёт, но это означает что в данный момент детище папы Карло лжёт, чего не может быть, так как мы уже выяснили, что утверждение правдиво. Значит, нос расти не должен, но если это не соответствует действительности, высказывание всё-таки истинно, а это в свою очередь свидетельствует, что Пиноккио лжёт… И так далее — цепочку взаимоисключающих причин и следствий можно продолжать до бесконечности.
Парадокс лжеца показывает противоречие высказывания в разговорной речи формальной логике. С точки зрения классической логики проблема неразрешима, поэтому утверждение «Я лгу» вообще не считается логическим.

Парадокс дней рождения.
Суть проблемы заключается в следующем: если существует группа из 23-х или более человек, вероятность того, что у двух из них дни рождения (число и месяц) совпадут, превышает 50%. Для групп от 60-ти человек шанс составляет свыше 99%, но 100% достигает, только если в группе не менее 367-ми человек (с учётом високосных лет). Об этом свидетельствует принцип Дирихле, названный по имени его открывателя, немецкого математика Петера Густава Дирихле.
Строго говоря, с научной точки зрения это утверждение не противоречит логике и поэтому не является парадоксом, зато оно отлично демонстрирует разницу результатов интуитивного подхода и математических расчётов, ведь на первый взгляд для столь небольшой группы вероятность совпадения кажется сильно завышенной.
Если рассматривать каждого члена группы по отдельности, оценивая вероятность совпадения его дня рождения с чьим-либо другим, для каждого человека шанс составит примерно 0,27%, таким образом, общая вероятность для всех членов группы должна быть около 6,3% (23/365). Но это в корне неверно, ведь количество возможных вариантов выбора определённых пар из 23-х человек гораздо выше числа её членов и составляет (23*22)/2=253, исходя из формулы вычисления так называемого числа сочетаний из данного множества. Не будем углубляться в комбинаторику, можете на досуге проверить правильность этих расчётов.
Для 253-х вариантов пар шанс, что месяц и дата рождения участников одной из них окажутся одинаковыми, как вы наверняка догадались, значительно больше 6,3%.

Проблема курицы и яйца.
Наверняка, каждому из вас хотя бы раз в жизни задавали вопрос: «Что появилось раньше — курица или яйцо?». Искушённые в зоологии знают ответ: птицы появлялись на свет из яиц задолго до возникновения среди них отряда куриных. Стоит отметить, что в классической формулировке говорится как раз о птице и яйце, но и она допускает лёгкое решение: ведь, например, динозавры появились раньше птиц, и они тоже размножались, откладывая яйца.
Если учесть все эти тонкости, можно сформулировать проблему следующим образом: что появилось ранее — первое животное, откладывающее яйца, или собственно его яйцо, ведь откуда-то должен был вылупиться представитель нового вида.
Главная проблема заключается в установке причинно-следственной связи между явлениями нечёткого объёма. Для более полного понимания этого ознакомьтесь с принципами нечёткой логики — обобщения классической логики и теории множеств.
Говоря упрощённо, дело в том, что животные в ходе эволюции прошли через бесчисленное количество промежуточных этапов — это касается и способов выведения потомства. На различных эволюционных стадиях они откладывали разные объекты, которые нельзя однозначно определить как яйца, но имеющие с ними некоторое сходство.
Вероятно, объективного решения этой проблемы не существует, хотя, например, британский философ Герберт Спенсер предложил такой вариант: «Курица — лишь способ, которым одно яйцо производит другое яйцо».

Источник


























 Каков шанс, что случайное число начнётся с цифры «1»? Или с цифры «3»? Или с «7»? Если вы немного знакомы с теорией вероятности, то можете предположить, что вероятность — один к девяти, или около 11%.
Каков шанс, что случайное число начнётся с цифры «1»? Или с цифры «3»? Или с «7»? Если вы немного знакомы с теорией вероятности, то можете предположить, что вероятность — один к девяти, или около 11%.


























 Этот парадокс был придуман древнегреческим философом Зеноном. Суть его такова: предположим, что Ахиллес бежит в 10 раз быстрее черепахи и находится за 1000 шагов от неё. Пока Ахиллес пробежит 1000 шагов, черепаха проползёт ещё 100 шагов. Когда Ахиллес пробежит 100 шагов, черепаха проползёт ещё 10 шагов, и так до бесконечности. В итоге Ахиллес так и не догонит черепаху. Естественно все мы понимаем, что в реальной жизни он бы её наверняка и догнал, и перегнал.
Этот парадокс был придуман древнегреческим философом Зеноном. Суть его такова: предположим, что Ахиллес бежит в 10 раз быстрее черепахи и находится за 1000 шагов от неё. Пока Ахиллес пробежит 1000 шагов, черепаха проползёт ещё 100 шагов. Когда Ахиллес пробежит 100 шагов, черепаха проползёт ещё 10 шагов, и так до бесконечности. В итоге Ахиллес так и не догонит черепаху. Естественно все мы понимаем, что в реальной жизни он бы её наверняка и догнал, и перегнал. Согласно древнегреческому мифу, жители Афин долгое время хранили корабль, на котором Тесей вернулся с острова Крит. Со временем корабль начал гнить, поэтому в нём постепенно начали менять доски. В определённый момент все доски корабля были заменены на новые. В итоге возник вполне закономерный вопрос: «Тот ли это ещё корабль или уже совсем другой?» Помимо этого, появился ещё один вопрос: «Что, если из старых досок собрать ещё один такой-же корабль, то какой из них будет настоящим?»
Согласно древнегреческому мифу, жители Афин долгое время хранили корабль, на котором Тесей вернулся с острова Крит. Со временем корабль начал гнить, поэтому в нём постепенно начали менять доски. В определённый момент все доски корабля были заменены на новые. В итоге возник вполне закономерный вопрос: «Тот ли это ещё корабль или уже совсем другой?» Помимо этого, появился ещё один вопрос: «Что, если из старых досок собрать ещё один такой-же корабль, то какой из них будет настоящим?» Предположим, у нас есть куча зёрен. Если из неё убирать по одному зерну, то когда она перестанет быть кучей? будет ли она кучей, если в ней останется только одно зерно? Объясняется парадокс тем, что у термина «куча» нет точного определения.
Предположим, у нас есть куча зёрен. Если из неё убирать по одному зерну, то когда она перестанет быть кучей? будет ли она кучей, если в ней останется только одно зерно? Объясняется парадокс тем, что у термина «куча» нет точного определения. Одному заключённому сказали: «Вас казнят в полдень следующей среды. Это будет неожиданностью для вас.» Заключённый приходит к выводу что раз он знает точное время казни, то казнь никак не сможет стать для него неожиданной, а значит его не смогут казнить. В полдень следующей среды за ним действительной приходит палач и его казнят. И казнь действительно ставится неожиданностью для заключённого.
Одному заключённому сказали: «Вас казнят в полдень следующей среды. Это будет неожиданностью для вас.» Заключённый приходит к выводу что раз он знает точное время казни, то казнь никак не сможет стать для него неожиданной, а значит его не смогут казнить. В полдень следующей среды за ним действительной приходит палач и его казнят. И казнь действительно ставится неожиданностью для заключённого.




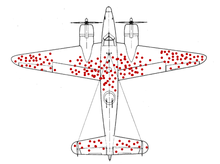
 Комбинированный вид
Комбинированный вид
