Прямые, кривые и очень изломанные. Краткая история линии от «Начал» Евклида до фракталов начала XX века
Что такое линия? Чем отличаются разные кривые друг от друга? Эти вопросы математики задают себе уже 2500 лет, и путь к ответам на них не лишен драматизма — открытие иррациональных длин отрезков было, по легенде, трагедией для мировоззрения пифагорейцев, а открытие заполняющих плоскость кривых Пеано в начале ХХ столетия заставило ученых пересмотреть свои представления о непрерывности и размерности пространства. Математик и художник Давид Кац — об истории понятия «кривая» в математике Античности и Средневековья и математическом анализе Нового времени.
Узоры древности
Интерес человека к прямым и искривленным линиям можно отследить с древнейших времен. Самые разные кривые мы видим в геометрических узорах на керамике и в архитектуре. Кроме достаточно простых узоров, составленных из прямых линий, часто можно встретить и что-то более сложное: спирали, волнистые линии и другие.


Представления о геометрии существовали уже в Египте и у цивилизаций Плодородного полумесяца. Возникли они, по-видимому, из совершенно практических потребностей: например, для сельского хозяйства важно уметь измерять площади участков земли. Однако в сохранившихся источниках мы видим эти представления скорее как набор рецептов, чем как науку.
Греция: длина без ширины
Древние греки подошли к вопросу более строго. В «Началах» Евклида возникают определения (впрочем, зачастую носящие скорее описательный характер — на них, например, не ссылаются далее) линии, прямой линии, точки. Выглядят они, мягко говоря, несовременно:
Определение 1.1. Точка — это то, часть чего есть ничто.
Определение 1.2. Линия — это длина без ширины.
Определение 1.3. Концы линий — это точки.
Определение 1.4. Прямая линия лежит равномерно по отношению к точкам на ней. (Или: Прямая линия есть та, которая равно лежит на всех своих точках.)
Первое из этих определений можно при желании трактовать в духе теории множеств, третье, по-видимому, намекает, что линии у нас априори конечные. Второе можно трактовать описательно, что касается четвертого, то мнения сильно расходятся.
Несколько иная, хотя местами и похожая ситуация возникает в труде, традиционно приписываемом Герону, — «Определение понятий геометрии» (но в статье W. R. Knorr, ‘Arithmêtikê stoicheiôsis’: on Diophantus and Hero of Alexandria, Historia Math. 20 (2) (1993), 180–192 приводятся аргументы в пользу принадлежности его Диофанту):
Прямая линия — это линия, которая одинакова по отношению ко всем точкам на ней, лежит прямо и максимально натянута между своими концами.
Последнее определение довольно явно отсылает нас к кратчайшему расстоянию между двумя точками.
Читайте также
Как описать весь мир с помощью математики?
В наиболее известных трудах древних греков рассматриваются главным образом прямые линии. Хотя в некоторых трудах встречаются и иные известные им линии.
Аполлоний Пергский, один из трех великих геометров Античности (вместе с Евклидом и Архимедом), занимался коническими сечениями. Об их существовании знали и до него, однако именно он дал им названия, закрепившиеся в науке, — эллипс, гипербола, парабола.
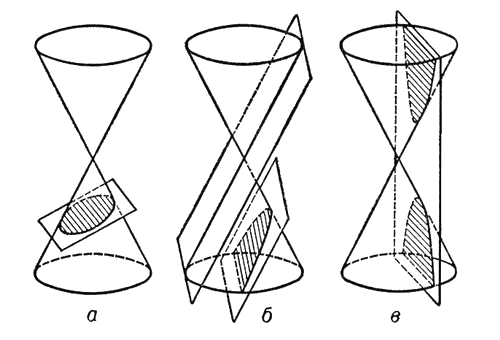
Приведем и несколько других примеров, известных грекам.
Циссоида Диокла:
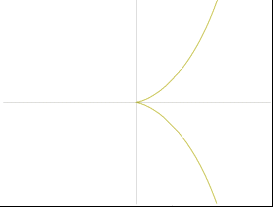
Конхоида Никомеда:
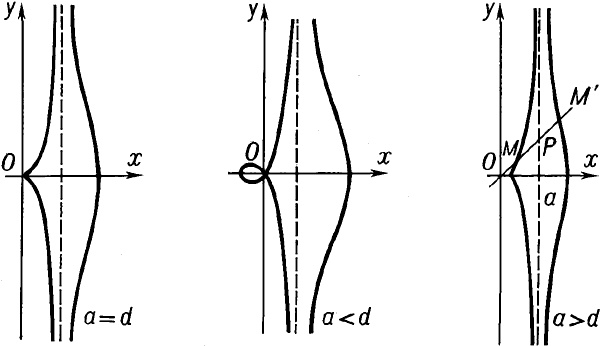
Знаменитая архимедова спираль:
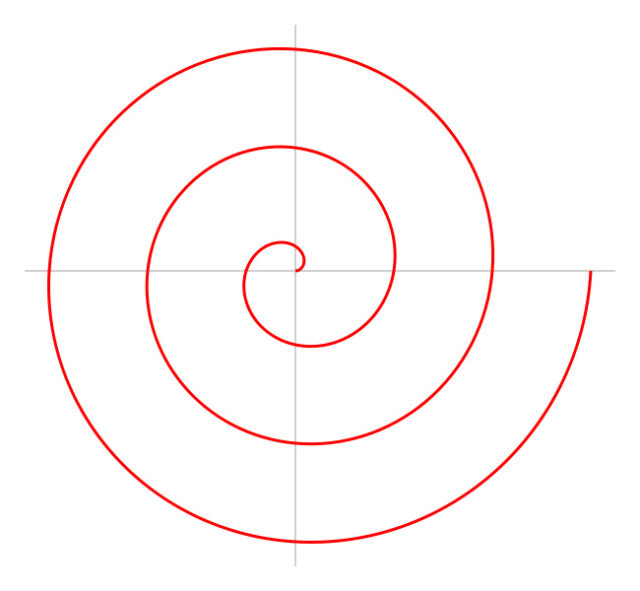 Вторжение иррационального
Вторжение иррационального
Кстати, даже в случае отрезков и прямых линий уже у греков возникли определенные проблемы. Давайте пройдем этот путь вместе с ними. Возьмем квадрат со стороной 1. Нетрудно посчитать, используя теорему Пифагора, что его диагональ будет равна корню из двух. Мы моментально попадаем в неловкую ситуацию: корень из двух (как мы знаем сейчас) — число иррациональное, а это значит, что если вы уменьшите сторону квадрата в целое число раз, то из полученных отрезков не сможете получить его диагональ: будет либо чуть больше, либо чуть меньше. Можно было бы сослаться здесь на неточность вычислений или измерений, но пифагорейцы получили этот результат вовсе не на практике, а из теоретических соображений. Доказательство их выглядело следующим образом:
Пусть есть квадрат ABCD. Предположим, существует такой отрезок, который укладывается m раз на диагонали AC и n раз на стороне AB. Тогда AC : AB = m : n. Без ограничения общности можно считать, что хотя бы одно из двух этих чисел нечетно (если это не так и оба четны, то пусть m = 2lm1, а n = 2kn1, где m1 и n1 нечетны; поделим m и n на минимальное из чисел 2l и 2k, получим два числа m′ и n′ такие, что AC : AB = m′ : n′ и по крайней мере одно из них нечетно. В дальнейшем вместо m′ и n′ будем писать m и n и считать, что одно из этих чисел нечетно).
Если построить квадрат со стороной AC (скажем, ACEF), то площадь этого квадрата будет относиться к площади квадрата ABCD как m2 к n2.
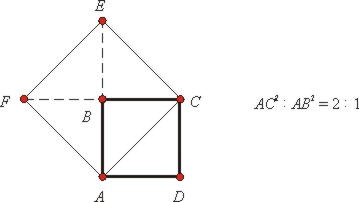 Согласно теореме Пифагора, площадь квадрата со стороной AC вдвое больше, чем площадь квадрата ABCD. Таким образом, m2 = 2n2. Значит, m — четное число. Пусть оно равно 2N. Тогда m2 = 4N2. Так как 4N2 = 2n2, n2 = 2N2. Значит, n — тоже четное. Это противоречит предположению о том, что одно из чисел m и n нечетно.
Согласно теореме Пифагора, площадь квадрата со стороной AC вдвое больше, чем площадь квадрата ABCD. Таким образом, m2 = 2n2. Значит, m — четное число. Пусть оно равно 2N. Тогда m2 = 4N2. Так как 4N2 = 2n2, n2 = 2N2. Значит, n — тоже четное. Это противоречит предположению о том, что одно из чисел m и n нечетно.
Для пифагорейцев это была печальная новость — в рамках арифметики им такие числа не встречались, поэтому казалось, что и в целом вычисления с длинами оказывались под угрозой.
Интересно, что позже, в рукописи «Выпрямляющий кривое» (в рамках нашей статьи это предельно интригующее название — чуть позже станет понятно почему) некоего Альфонсо, предположительно, крещеного еврея, жившего в Испании между XIII и XV веками, к несоразмерности длин отношение уже гораздо более доброжелательное:
«Следует знать, что от ученых не скрыто то, как поступают люди, которые обвивают прямыми тонкими нитями из шелка, или льна, или другого материала скрепленный круг и измеряют его окружность прямой линией. Однако следует знать, будет ли на самом деле так, как это воспринимается чувством, которое обладает приблизительностью, ибо чувство недостаточно для этого при той приблизительности, которая имеется в нем. Ведь всякие две линии, не равные друг другу, можно разрезать на очень маленькие части так, что чувством будут их воспринимать как равноценные. Вместе с тем возможно, что эти величины несоизмеримы и что видов иррациональной меры бесконечное количество, как это доказано в 10-й книге Евклида».
Координаты и разрывы
Значительное развитие в понимании кривых линий произошло с переходом от геометрического описания к алгебраическому — в частности, к описанию кривых через уравнения.
В действительности нечто похожее на уравнение встречается у Архимеда и Аполлония Пергского — это так называемые симптомы конических сечений.
Затем координаты (в виде заимствованных из географии понятий долготы и широты) встречаются у Николая Орезмского во второй половине XIV столетия. В XVI веке Виет начал использовать символы для записи уравнений. И, наконец, Рене Декарт (синхронно с ним — Пьер де Ферма) развил идеи, совмещающие символьную запись уравнений и систему координат. Его труд пользовался огромной популярностью и быстро получил широкое распространение и существенное развитие. В системе координат появились отрицательные значения, саму сетку координат научились строить косоугольной.
Этот подход, хотя и ограниченно, применял Ньютон. Впоследствии Кеплер для представления траекторий движения планет активно использовал конические сечения в координатах, геометрически описанные еще греками.
Предыдущие шаги сформировали понятие алгебраической кривой — множества точек, чьи координаты связаны уравнением кривой.
Интересно, что уже на этом, алгебраическом уровне возникают кривые с любопытными особенностями. Возьмем, например, известную многим со школы гиперболу — график функции 1/x. Его можно построить по точкам, но несложно сообразить, что уравнение y = 1/x имеет решение для любого x, кроме одного: x = 0 (на ноль делить нельзя). Это сказывается и на графике:
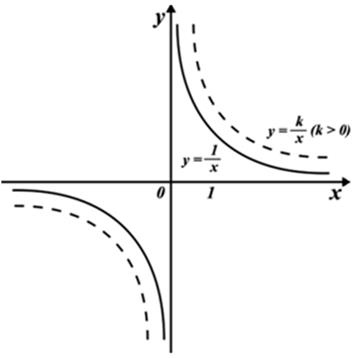
Что происходит в окрестности нуля? Нетрудно ответить. Давайте подойдем к нему справа. Когда мы подставляем в качестве x в выражение 1/x целое число больше 1, мы получаем дробь. Чем больше число, тем меньше получается дробь — этим и объясняется то, что график идет всё ниже и ниже по мере продвижения вправо. Подставляем х = 100, получаем у = 1/100, подставляет 1000000, получаем 1/1000000. Когда мы подставим в выражение единицу, на выходе получим единицу. Теперь пойдем в обратную сторону, ближе к нулю. Когда мы подставляем в выражение для y ½, она попадает в нижнюю часть дроби. Как мы помним, когда мы делим что-то на дробь, нам нужно умножить на перевернутую эту дробь. Значит, мы получим 2. Очевидно, чем ближе мы к нулю, тем сильнее уходим вверх — подставив 1/1000000, мы получим у = 1000000. Похожая ситуация при подходе слева, но с отрицательным знаком.
То, что происходит в нуле, называется разрывом (по виду графика хорошо понятно почему). В анализе принято классифицировать точки разрыва особым образом. То, что мы сейчас видели, называется точкой разрыва второго рода, поскольку односторонние пределы с двух сторон бесконечны (достаточно того, что один из них бесконечен). Если же односторонние пределы в точке разрыва конечны, то такая точка называется точкой разрыва первого рода.
Длина кривой
С самого начала людям хотелось описывать не только сами объекты, но и их свойства. И раз уж мы говорим о «длине, лишенной ширины», хотелось бы уметь эту длину считать. Мы хорошо умеем считать длины прямых отрезков при помощи линейки, которая позволяет нам определять расстояние между двумя точками, но когда дело касается кривых линий, нам нужен иной метод.
Мы расставляем n точек на равном расстоянии вдоль кривой, после чего замеряем длину прямых отрезков между этими точками (это мы делать умеем). Интуитивно возникает подозрение, что с увеличением числа n мы будем приближаться к значению настоящей длины — прирост суммы будет всё меньше, сверху он ограничен настоящей длинной кривой.
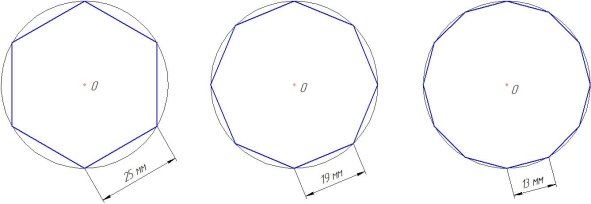
Для простых примеров — скажем, окружностей, синусоид, парабол — этот подход отлично работает. Примеры, в которых он дает сбой, мы рассмотрим далее.
Гладкость
Еще одним свойством, характеризующим кривые, является гладкость. Хотя смысл слова интуитивно понятен, задать ее математически не совсем элементарно. Мы хотим, чтобы у кривой не было углов, заострений, клювов и т. п.
Хороший пример гладкой кривой — синусоида:
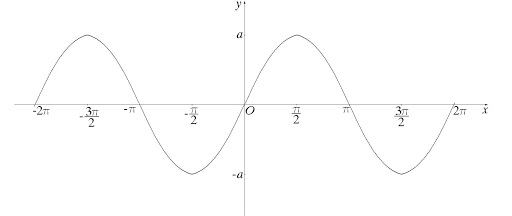
А вот пример негладкой кривой:
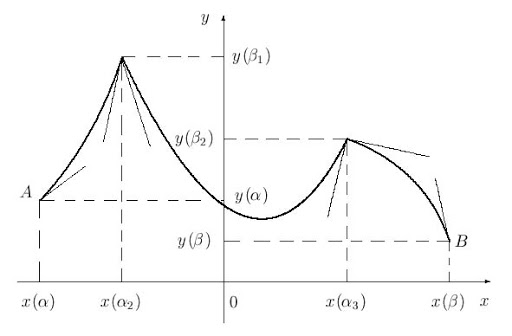
Чтобы определить это свойство, разберемся, что оно означает геометрически. Для начала вспомним концепцию касательной. Обычно в школе рассматривают в первую очередь касательные окружностей и определяют их как прямые, имеющие одну общую точку с окружностью. В случае произвольной кривой рассматривается касательная в локальном смысле — пересечения кривой вне некоторой окрестности точки касания не рассматриваются как проблема.
В курсе начал анализа доказывается, что такая касательная неразрывно связана с производной функции, график которой образует нашу кривую: более конкретно — тангенс угла наклона касательной (по отношению к положительному направлению оси Ox) равен значению производной функции в точке касания.
Эта связь позволяет нам четко определить гладкость функции. Чтобы функция называлась гладкой (и, следовательно, ее график был гладкой кривой), необходимо, чтобы, во-первых, эта функция была непрерывной, во-вторых, ее производная должна существовать и быть непрерывной.










 Представления о геометрии существовали уже в Египте и у цивилизаций Плодородного полумесяца. Возникли они, по-видимому, из совершенно практических потребностей: например, для сельского хозяйства важно уметь измерять площади участков земли. Однако в сохранившихся источниках мы видим эти представления скорее как набор рецептов, чем как науку.
Представления о геометрии существовали уже в Египте и у цивилизаций Плодородного полумесяца. Возникли они, по-видимому, из совершенно практических потребностей: например, для сельского хозяйства важно уметь измерять площади участков земли. Однако в сохранившихся источниках мы видим эти представления скорее как набор рецептов, чем как науку. Приведем и несколько других примеров, известных грекам.
Приведем и несколько других примеров, известных грекам. Конхоида Никомеда:
Конхоида Никомеда: Знаменитая архимедова спираль:
Знаменитая архимедова спираль: Вторжение иррационального
Вторжение иррационального Согласно теореме Пифагора, площадь квадрата со стороной AC вдвое больше, чем площадь квадрата ABCD. Таким образом, m2 = 2n2. Значит, m — четное число. Пусть оно равно 2N. Тогда m2 = 4N2. Так как 4N2 = 2n2, n2 = 2N2. Значит, n — тоже четное. Это противоречит предположению о том, что одно из чисел m и n нечетно.
Согласно теореме Пифагора, площадь квадрата со стороной AC вдвое больше, чем площадь квадрата ABCD. Таким образом, m2 = 2n2. Значит, m — четное число. Пусть оно равно 2N. Тогда m2 = 4N2. Так как 4N2 = 2n2, n2 = 2N2. Значит, n — тоже четное. Это противоречит предположению о том, что одно из чисел m и n нечетно. Предыдущие шаги сформировали понятие алгебраической кривой — множества точек, чьи координаты связаны уравнением кривой.
Предыдущие шаги сформировали понятие алгебраической кривой — множества точек, чьи координаты связаны уравнением кривой.
 Для простых примеров — скажем, окружностей, синусоид, парабол — этот подход отлично работает. Примеры, в которых он дает сбой, мы рассмотрим далее.
Для простых примеров — скажем, окружностей, синусоид, парабол — этот подход отлично работает. Примеры, в которых он дает сбой, мы рассмотрим далее. А вот пример негладкой кривой:
А вот пример негладкой кривой: Чтобы определить это свойство, разберемся, что оно означает геометрически. Для начала вспомним концепцию касательной. Обычно в школе рассматривают в первую очередь касательные окружностей и определяют их как прямые, имеющие одну общую точку с окружностью. В случае произвольной кривой рассматривается касательная в локальном смысле — пересечения кривой вне некоторой окрестности точки касания не рассматриваются как проблема.
Чтобы определить это свойство, разберемся, что оно означает геометрически. Для начала вспомним концепцию касательной. Обычно в школе рассматривают в первую очередь касательные окружностей и определяют их как прямые, имеющие одну общую точку с окружностью. В случае произвольной кривой рассматривается касательная в локальном смысле — пересечения кривой вне некоторой окрестности точки касания не рассматриваются как проблема.






 Древовидный вид
Древовидный вид