Теоретические основы математического моделирования.
Сегодня
Теоретические основы математического моделирования.
Философскую концепцию моделирования составляют теория отражения и теория познания, а формально-методическую основу моделирования составляют теория подобия, теория эксперимента, математическая статистика, математическая логика и научные дисциплины, изучающие те предметные области, которые подлежат исследованию методами моделирования.
Согласно математической
теории подобия абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании большинства систем (за исключением, возможно, моделирования одних математических структур другими) абсолютное подобие невозможно, и основная цель моделирования - модель достаточно хорошо должна отображать функционирование моделируемой системы. Одними из основных понятий, используемых в моделировании, являются понятия изоморфизма и гомоморфизма.
Изоморфизм и гомоморфизм (греч.
isos — одинаковый,
homoios — подобный и
morphe — форма) — понятия, характеризующие соответствие между структурами объектов.
Две системы, рассматриваемые отвлеченно от природы составляющих их элементов, являются
изоморфными друг другу, если каждому элементу первой системы соответствует лишь один элемент второй и каждой связи в одной системе соответствует связь в другой и обратно. Такое взаимно-однозначное соответствие называется изоморфизм (Рис. 3).
 Рис. 3. К понятию изоморфизма
Рис. 3. К понятию изоморфизма
Изоморфизм связан не со всеми, а лишь с некоторыми выбранными в процессе анализа свойствами объектов, которые в других своих отношениях могут отличаться.
Гомоморфизм отличается от изоморфизма тем, что соответствие объектов однозначно лишь в одну сторону. Поэтому гомоморфный образ есть неполное, приближенное отображение структуры оригинала. Примерами гомоморфизма могут служитьотношение между картой и местностью или отношение между грамзаписью и ее оригиналом.
Математическая модель представляет собой некоторую абстракцию реального объекта и строится как описание последнего на основе использования основных категорий и понятий. Рассмотрим эти понятия.
Под
предметной областью будем понимать мысленно ограниченную область реальной действительности или область идеальных представлений, подлежащую описанию (моделированию) и исследованию. Предметная область состоит из объектов, различаемых по каким-либо признакам (свойствам) и находящихся в определенных отношениях между собой, или взаимодействующих каким-либо образом (Рис. 4).
 Рис. 4. К понятиям объект, свойство, показатель
Под объектом
Рис. 4. К понятиям объект, свойство, показатель
Под объектом понимается нечто целое, которое реально существует или возникает в нашем сознании, и обладающее свойствами, значения которых позволяют нам однозначно распознавать это целое. Объект, на котором сосредоточивается внимание субъекта с целью исследования, называется
объектом исследования.
Объекты воспринимаются и различаются субъектами лишь постольку, поскольку они обладают характерными свойствами.
Свойством называется характерная особенность объекта, которая может быть замечена и оценена субъектом, например, вес, цвет, длина, плотность и тому подобное.
Для оценки исследуемого свойства объекта субъект устанавливает определенную меру называемую
показателем свойства. Для каждого показателя определяется множество значений (уровней, или градаций меры свойства), которые присваиваются ему в результате оценивания свойства. Таким образом, свойство объекта является реальностью, а показатель - субъективной мерой этой реальности (если речь идет о реальных объектах).
Показатели всеобщих свойств материальных объектов, таких как пространство и времяназываются
основными показателями. Подавляющее большинство показателей других свойств выражаются через показатели этих основных свойств. Поэтому единицы измерения основных показателей служат основой для построения стандартной системы единиц измерения физических величин и называются основными единицами измерения.
Выражение показателя некоторого свойства через основные единицы измерения, принятые в определенной стандартной системе единиц (мер), называется
размерностью данного показателя.
Свойства делятся на
внутренние (собственные) свойства объектов, показатели которых называются
параметрами, и
внешние, представляющие собой свойства среды, связанные некоторыми отношениями с параметрами данного объекта, показатели которых называются
факторами.
Свойства объектов выявляются только при их взаимодействии, или при сопоставлении объектов друг с другом. Сопоставление (комбинация) значений показателей, наблюдаемых свойств определенных объектов называется
отношением. Говорят, что отношение
истинно, если оно подтверждается практическим экспериментом, или логическим выводом. Отношение считается
ложным, если оно опровергается практической проверкой, или логическим выводом. В противном случае отношение считается неопределенным. Понятия «истинно», «ложно», «неопределенно» являются логическими значениями любого отношения, результатами субъективной его оценки.
Взаимодействие объектов определяется по результатам измерения значений показателей наблюдаемых свойств этих объектов. Поэтому каждому действию, или взаимодействию присваивается определенный результат. Это может быть значение, или определенная комбинация значений показателей свойств взаимодействующих объектов. Действия над значениями показателей свойств объектов, выполняемые по определенным правилам и приводящие к предполагаемому результату, называются
операцией или процедурой.
Значения показателей свойств объектов обозначаются символами из некоторого заранее определенного множества
А, называемого
алфавитом.
Множество объектов, взаимосвязанных между собой определенными отношениями, и выполняющих определенную общую для них целевую функцию или имеющих общее предназначение, называется
системой.
Система, состоящая из алфавита
А, строго определенных множеств отношений
G, операций
Q и предназначенная для символического описания объектов и систем определенного класса, называется
формальной системой. Такие системы положены в основу языков математического моделирования.
Энергия является одним из свойств материи, в силу которого все материальные объекты совершают движение в пространстве и времени, находясь в энергетическом взаимодействии и пространственно-временном отношении.
Все материальные объекты существуют в
пространстве и во
времени, которые также являются всеобщими свойствами материи. Значения показателей пространства и времени входят в состав основных единиц измерения физических свойств объектов.
Так как все свойства объектов изменяются во времени, то любой набор значений показателей этих свойств относится к определенному значению показателя времени. Это отношение называется
состоянием объекта.
Значения показателей свойств со временем меняются, в результате чего происходит смена состояний объектов. Акт смены состояний объекта, отнесенный к определенному промежутку времени, называется
событием, а последовательность взаимосвязанных событий, происходящих на некотором интервале времени, называется
процессом.
Моделирование (в значении «метод», «модельный эксперимент») рассматривается как особая форма эксперимента, эксперимента не над самим оригиналом (это называется простым или обычным экспериментом), а над копией (заместителем) оригинала. В связи с этим одной из основных задач, решаемых в процессе исследований, является задача построения экспериментального образца, т.е., модели исследуемой системы, процесса или явления. Эта задача реализуется в идее совокупности шагов (этапов), целями которых являются сбор данных об исследуемой системе, создание содержательного описания, его формализация, разработка компьютерной программы и обоснование действующей программной модели.
На созданной модели проводится изучение моделируемой системы (оригинала) путем ряда запусков программы (прогонов) на совокупности исходных данных. Собранные сведения анализируются и документируются.
На рис. 5 показаны основные этапы, из которых состоит процесс моделирования.
 Рис. 5. Основные этапы математического моделирования
Рис. 5. Основные этапы математического моделирования
Выполнение шагов описанной процедуры не является в общем случае строго последовательным: в зависимости от получаемых на одном из шагов результатов возможен возврат на предыдущие шаги с целью корректировки их результатов с последующим их повторением. Иначе говоря, процесс моделирования носит
итеративный характер.









 Представления о геометрии существовали уже в Египте и у цивилизаций Плодородного полумесяца. Возникли они, по-видимому, из совершенно практических потребностей: например, для сельского хозяйства важно уметь измерять площади участков земли. Однако в сохранившихся источниках мы видим эти представления скорее как набор рецептов, чем как науку.
Представления о геометрии существовали уже в Египте и у цивилизаций Плодородного полумесяца. Возникли они, по-видимому, из совершенно практических потребностей: например, для сельского хозяйства важно уметь измерять площади участков земли. Однако в сохранившихся источниках мы видим эти представления скорее как набор рецептов, чем как науку.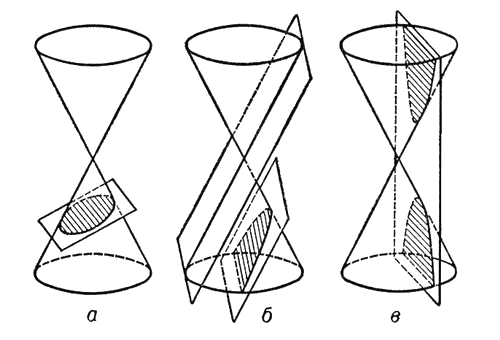 Приведем и несколько других примеров, известных грекам.
Приведем и несколько других примеров, известных грекам. Конхоида Никомеда:
Конхоида Никомеда: Знаменитая архимедова спираль:
Знаменитая архимедова спираль: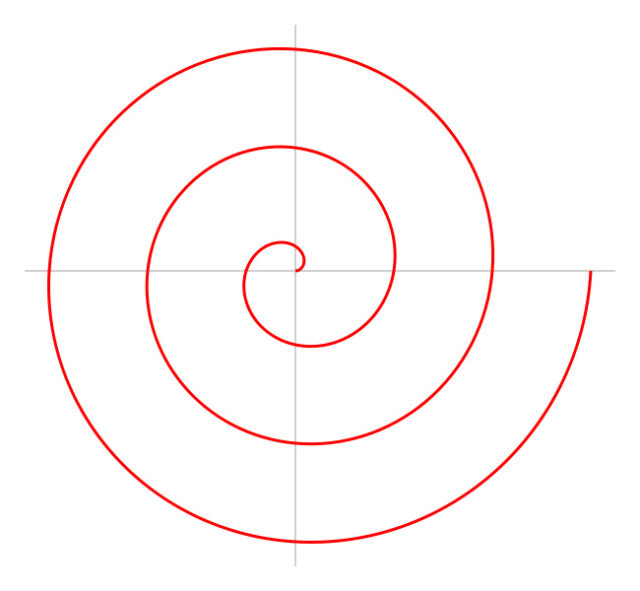 Вторжение иррационального
Вторжение иррационального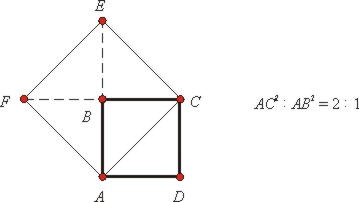 Согласно теореме Пифагора, площадь квадрата со стороной AC вдвое больше, чем площадь квадрата ABCD. Таким образом, m2 = 2n2. Значит, m — четное число. Пусть оно равно 2N. Тогда m2 = 4N2. Так как 4N2 = 2n2, n2 = 2N2. Значит, n — тоже четное. Это противоречит предположению о том, что одно из чисел m и n нечетно.
Согласно теореме Пифагора, площадь квадрата со стороной AC вдвое больше, чем площадь квадрата ABCD. Таким образом, m2 = 2n2. Значит, m — четное число. Пусть оно равно 2N. Тогда m2 = 4N2. Так как 4N2 = 2n2, n2 = 2N2. Значит, n — тоже четное. Это противоречит предположению о том, что одно из чисел m и n нечетно. Предыдущие шаги сформировали понятие алгебраической кривой — множества точек, чьи координаты связаны уравнением кривой.
Предыдущие шаги сформировали понятие алгебраической кривой — множества точек, чьи координаты связаны уравнением кривой.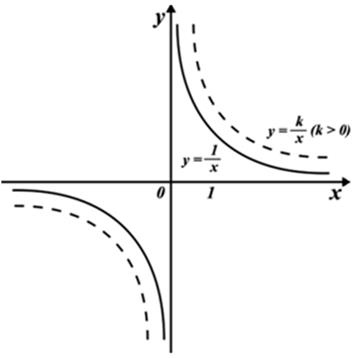
 Для простых примеров — скажем, окружностей, синусоид, парабол — этот подход отлично работает. Примеры, в которых он дает сбой, мы рассмотрим далее.
Для простых примеров — скажем, окружностей, синусоид, парабол — этот подход отлично работает. Примеры, в которых он дает сбой, мы рассмотрим далее. А вот пример негладкой кривой:
А вот пример негладкой кривой: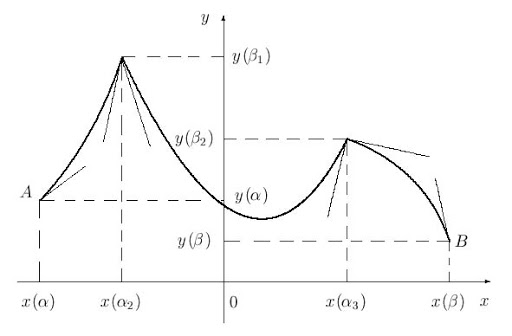 Чтобы определить это свойство, разберемся, что оно означает геометрически. Для начала вспомним концепцию касательной. Обычно в школе рассматривают в первую очередь касательные окружностей и определяют их как прямые, имеющие одну общую точку с окружностью. В случае произвольной кривой рассматривается касательная в локальном смысле — пересечения кривой вне некоторой окрестности точки касания не рассматриваются как проблема.
Чтобы определить это свойство, разберемся, что оно означает геометрически. Для начала вспомним концепцию касательной. Обычно в школе рассматривают в первую очередь касательные окружностей и определяют их как прямые, имеющие одну общую точку с окружностью. В случае произвольной кривой рассматривается касательная в локальном смысле — пересечения кривой вне некоторой окрестности точки касания не рассматриваются как проблема.
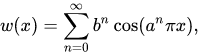 здесь a — любое нечетное число кроме единицы, b — число от нуля до единицы, а большая греческая cигма обозначает суммирование. Функция оказывается непрерывной для всех вещественных х, но при ряде условий на a и b очень негладкой:
здесь a — любое нечетное число кроме единицы, b — число от нуля до единицы, а большая греческая cигма обозначает суммирование. Функция оказывается непрерывной для всех вещественных х, но при ряде условий на a и b очень негладкой: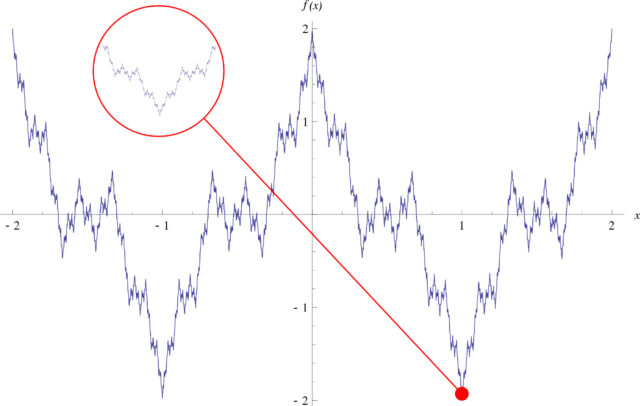 Бесконечность в глубине отрезка
Бесконечность в глубине отрезка Впоследствии Кнопп построил жорданову кривую, обладающую ненулевой площадью вдоль всей кривой. Этот результат достигается за счет очень узких вырезаемых «клиньев», узость которых приводит к тому, что вычитаемая из площади треугольника площадь падает экспоненциально.
Впоследствии Кнопп построил жорданову кривую, обладающую ненулевой площадью вдоль всей кривой. Этот результат достигается за счет очень узких вырезаемых «клиньев», узость которых приводит к тому, что вычитаемая из площади треугольника площадь падает экспоненциально.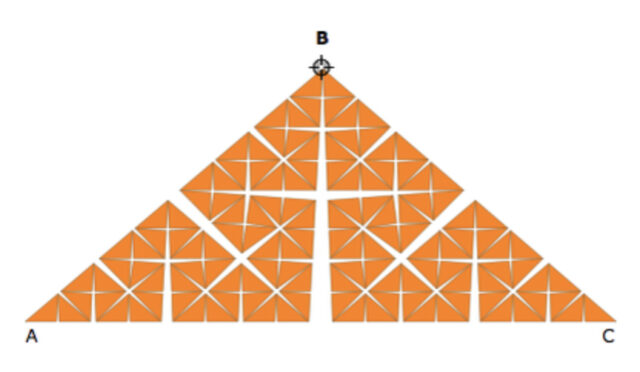 Кстати, вот
Кстати, вот 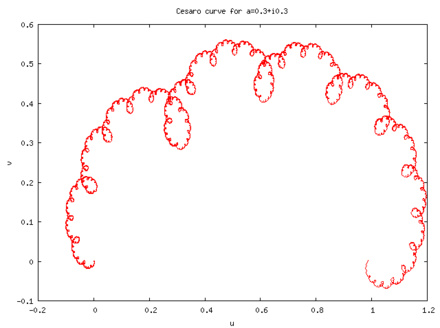 кривую Коха — Пеано
кривую Коха — Пеано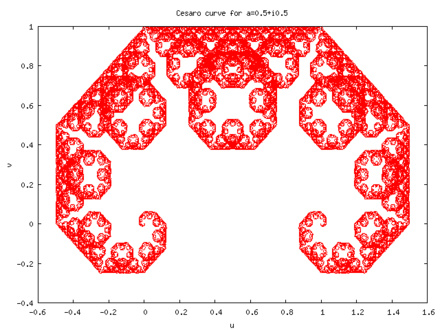 и еще несколько кривых де Рама:
и еще несколько кривых де Рама: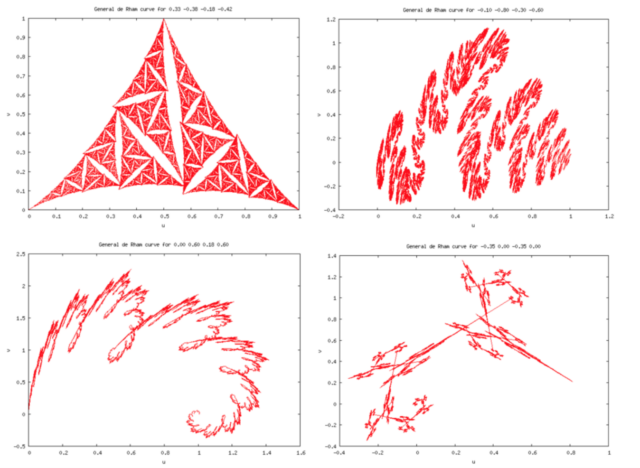 Заполнить плоскость
Заполнить плоскость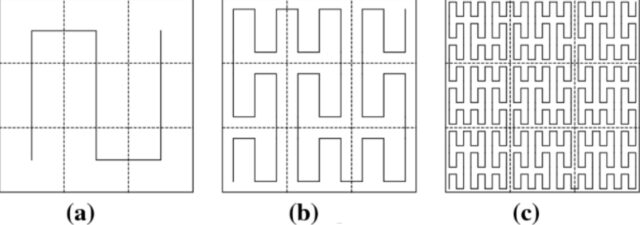 Обратите внимание на клетки, они позволяют понять, что происходит на каждом участке. То, что получится в результате бесконечного процесса этого рода, и называется кривой Пеано.
Обратите внимание на клетки, они позволяют понять, что происходит на каждом участке. То, что получится в результате бесконечного процесса этого рода, и называется кривой Пеано.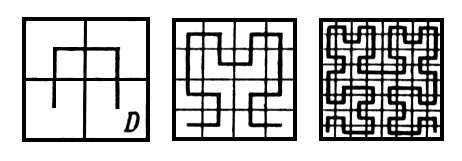 Существуют и объемные, и многомерные аналоги кривой Пеано, заполняющие куб (многомерный куб, соответственно).
Существуют и объемные, и многомерные аналоги кривой Пеано, заполняющие куб (многомерный куб, соответственно).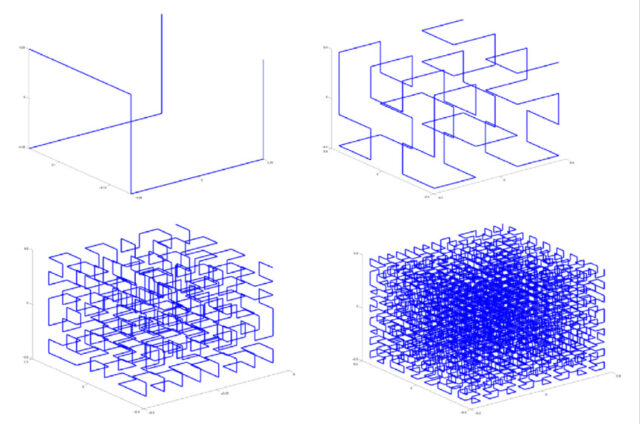


 Фракталы
Фракталы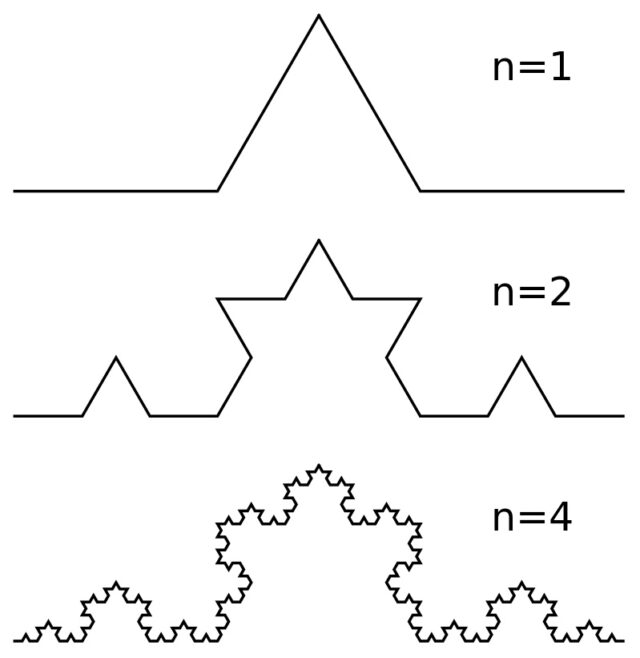 В качестве нулевого «поколения» берем просто отрезок. На первом шаге его среднюю треть превращаем в правильный треугольник без основания, как бы выгибаем его. У нас получится четыре соединенных в кривую линию отрезка. На следующем шаге повторяем эту операцию с каждым из четырех отрезков. И так далее до бесконечности.
В качестве нулевого «поколения» берем просто отрезок. На первом шаге его среднюю треть превращаем в правильный треугольник без основания, как бы выгибаем его. У нас получится четыре соединенных в кривую линию отрезка. На следующем шаге повторяем эту операцию с каждым из четырех отрезков. И так далее до бесконечности.




 Линейный вид
Линейный вид

