Золотые Стихи Пифагора
Мгновения Феано
Для Пифагора высшей целью человека
Являлась творческая Цельная волна,
Апофеоз игры Творца, Его ума,
Сознанье божеское, знание секрета...
"Золотые стихи" содержат в себе ту часть эзотерического учения Пифагора,
которую он и его последователи признали возможным открыть непосвященным.
Лизий, его ученик, после разгрома чернью пифагорейских общин в Великой
Греции, принес эти стихи с собою в Элладу, где завещал своим единомышленникам
читать их ежедневно утром и вечером. О том, что правило это соблюдалось у
пифагорейцев в течение целого ряда веков, мы знаем от Цицерона, Горация,
Сенеки, Галиена и других древних писателей.
Сохранились они для нас лишь в
комментариях Гиероклеса и в отрывках у классиков и Отцов Церкви.
Сообразно трем степеням посвящения, стихи эти разделялись на три части:
"Приготовление",
"Очищение" и
"Совершенствование".
На Семи Морях - музыкальная страничка -
http://sseas7.narod.ru/pifzol.htm
Стихи актуальны для молодежи любого времени, просты и мудры,
несут в себе основы знания галактической этики и счастливой жизни.
ЗОЛОТЫЕ СТИХИ ПИФАГОРЕЙЦЕВ
ПРОГОТОВЛЕНИЕ
Прежде всего, почитай волю бессмертных богов.
Их старшинство соблюдай в свете Закона веков.
((()))
Верен будь клятве, внимай, демонов остерегайся,
Мать и Отца уважай, добрым быть, честным старайся.
ОЧИЩЕНИЕ
Клятва - закон, сознавай. Лживости, лени беги,
Солнце душою встречай, честь, словно жизнь, береги.
((()))
С доблестным дружбу крепи, Людям стремись помогать.
Мелких обид уходи, незачем зло вспоминать.
((()))
Необходимость где, там есть и возможность всегда.
Внемли ты этим словам, будут успешней года…
((()))
Все это так и запомни. В пище умеренным стань.
Сон ограничь и дополни делом, ворчать перестань.
((()))
Гнев обуздай и желанья. Не совершай ничего
Стыдного, эти деянья след оставляют, клеймо.
((()))
Пусть повторяют в веках: Главный судья – это Совесть!
Тем, кто бессовестен – крах. Правда - вот лучшая доблесть.
((()))
Только запомни, кончина неотвратима для смертных.
Все, что в судьбе, не кручина - опыт и знание верных.
((()))
Смертным по воле богов могут прийти и страданья,
Может быть беден твой кров, это все лишь испытанье.
((()))
Ропот смири на судьбу и утешенья ищи
Там, где взойдет поутру солнышко мудрой тиши.
((()))
Честные люди, пойми, меньше невзгодам подвластны.
Веры слепой не ищи, многие речи - напрасны.
((()))
Часто за правду обман слепо, увы, принимают.
Ты же иди сквозь туман к свету, где Истину знают.
((()))
Не доверяйся тому, кто ненадежен в делах,
Лучше дай время уму, не торопясь на словах.
((()))
Прежде, чем делать, подумай! Глупость выходит тогда,
Коли забавой неумной ты опозоришь себя.
((()))
Делай всегда только то, что не ведет к сокрушенью.
Если не знаешь чего, остерегись совершенья.
((()))
Но изучай все вокруг - жизнь твоя станет прекрасной.
Не оставляй свой недуг без излеченья, неясным.
((()))
Меру во всем соблюдай, и в упражнениях тела.
Роскоши, зла избегай, зависти, дерзкого дела.
((()))
Лишних расходов беги, но и не слишком скупись.
Меру во всем обрети. Думай пред делом, трудись.
СОВЕРШЕНСТВО
Прежде, чем в сон погрузиться, вспомни о каждом поступке,
Что совершил. Не годится делать поблажки минутке.
((()))
Все ты в уме перечти, прежде, чем очи закрыть.
Все обсуди и спроси сам себя, чтоб не забыть.
- Что я не сделал и как там или тут поступил?
Сам я себе ли не враг? Все ли исправил, простил?
((()))
Так ты отыщешь пути для достижения цели.
Клятвы и тайны храни, веру в успех на пределе.
((()))
Так поступай и усвой… все, к чему должен стремиться,
Путь достижения твой… может с божественным слиться.
((()))
Кто четверицу открыл, жизни источник наш вечный,
Тот о тебе не забыл! Ты же трудись, друг сердечный.
((()))
Так за работу берись, чтобы увидеть конец,
Мудрым богам помолись, помня единство сердец.
((()))
Все мирозданье бессмертных в смертных чертах постигай.
Что преходяще - в мгновенных сроках коротких узнай.
((()))
И о единстве Природы, и о сокрытом в веках
Думай... Веками народы мысли хранили в стихах.
((()))
Станет понятно: несчастье люди приносят себе
Сами... слепые до счастья, сами... глухие во тьме.
((()))
Путь совершенства доступен каждому, все же не знают,
Где от страданья заступник. Так и рассудок теряют.
((()))
Злая судьба их кидает с места на место. Раздор
Людям таким предвещает, беды, а следом позор.
Ты ж уклонись от таких. Зевс, твой великий Отец,
Даст пониманье благих качеств Природы, сердец.
((()))
Высшей Природы начало в каждом присутствует, знай.
В смертных бессмертья причалы, дверь к божеству отворяй.
((()))
Все открывает Природа! Если наказы исполнишь,
То не коснутся невзгоды, истиной разум наполнишь.
Душу от множества бедствий ты охранишь и спасешь
Тем от забвенья наследство. Знанья веков обретешь.
((()))
К Истине путь - твой возничий. Знания - лучший твой друг!
Даже в эфирном обличье выйдешь за смертный сей круг.
((()))
Станешь нетленным и вечным, смерти не знающим богом.
***
Наставления Пифагора, Сказка о Душе,
Акусмы Пифагора и Учение в ритмах -
в Море Пифагора - сайт Семь Морей.
***
Опубликованы Золотые стихи на авторском сайте Сказки мудрецов в 2003 году.
Там же имеются и переводы Золотых Стихов другими авторами, и комментарии к Золотым Стихам.
Золотые стихи с комментариями Гиерокла
Золотые стихи в ритмах Феано
Золотые стихи в переводе Е.П.Казначеевой
Золотые стихи в переводе И. Евсы
Река речений Пифагора
http://feano.yorik.su/ezop/16972.html

Феана
http://sseas7.narod.ru/03.htm








 Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым - Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и сделал.
Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым - Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и сделал.
 Кантор (крупнейший немецкий историк математики) считает, что равенство
Кантор (крупнейший немецкий историк математики) считает, что равенство
 Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой-на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод:
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой-на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод: Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
 Доказательство Нильсена.
Доказательство Нильсена.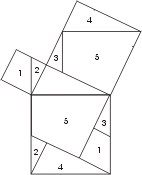 Доказательство Бетхера .
Доказательство Бетхера .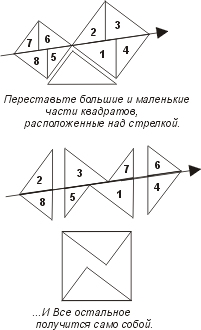
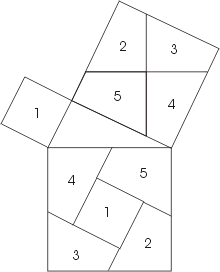 Доказательство Гутхейля.
Доказательство Гутхейля.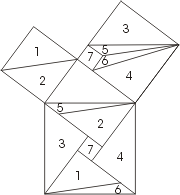 Доказательство 9 века н.э.
Доказательство 9 века н.э.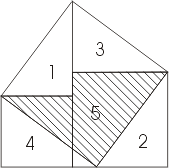
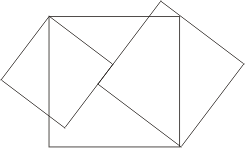
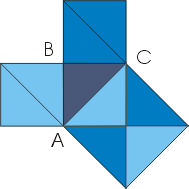
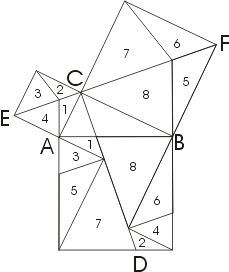
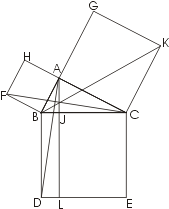
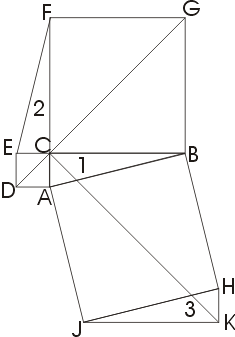 Поясним этот метод на примере. На рис. к обычной пифагоровой фигуре приставлены сверху и снизу треугольники 2 и 3, равные исходному треугольнику 1. Прямая DG обязательно пройдет через C. Заметим теперь (далее мы это докажем), что шестиугольники DABGFE и CAJKHB равновелики. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат,построенный на гипотенузе. Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов,построенных на катетах.
Поясним этот метод на примере. На рис. к обычной пифагоровой фигуре приставлены сверху и снизу треугольники 2 и 3, равные исходному треугольнику 1. Прямая DG обязательно пройдет через C. Заметим теперь (далее мы это докажем), что шестиугольники DABGFE и CAJKHB равновелики. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат,построенный на гипотенузе. Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов,построенных на катетах.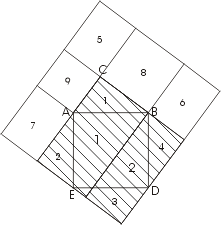
 Упрощенное доказательство Евклида
Упрощенное доказательство Евклида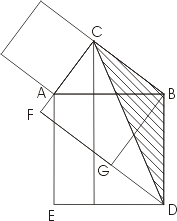 Доказательство Хоукинсa.
Доказательство Хоукинсa.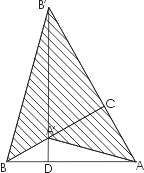 Доказательство Вальдхейма.
Доказательство Вальдхейма.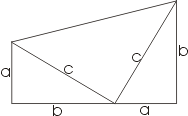
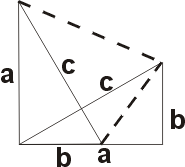 Доказательство основанное на теории подобия.
Доказательство основанное на теории подобия.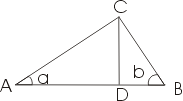 Доказательство индийского математика Басхары изображено на рисунке. В пояснение к нему он написал только одну строчку: "Смотри!". Ученые считают, что он выражал площадь квадрата ,построенного на гипотенузе, как сумму площадей треугольников (4ab/2) и площадь квадрата (a-b)². Следовательно:
Доказательство индийского математика Басхары изображено на рисунке. В пояснение к нему он написал только одну строчку: "Смотри!". Ученые считают, что он выражал площадь квадрата ,построенного на гипотенузе, как сумму площадей треугольников (4ab/2) и площадь квадрата (a-b)². Следовательно: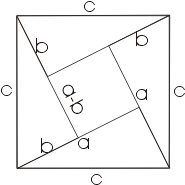 Луночки Гиппократа
Луночки Гиппократа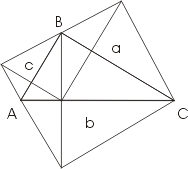 Познакомимся с одним интересным предложением, которое встречается во многих учебниках геометрии под названием теоремы о Гиппократовых луночках.
Познакомимся с одним интересным предложением, которое встречается во многих учебниках геометрии под названием теоремы о Гиппократовых луночках.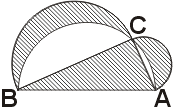 Векторное док-во
Векторное док-во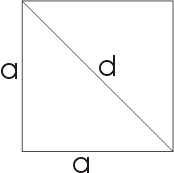 Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем
Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем 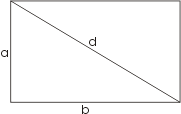 Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а другой катет a/2. Таким образом имеем
Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а другой катет a/2. Таким образом имеем 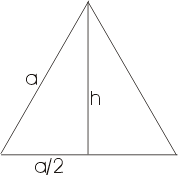 Возможности применения теоремы Пифагора к вычислениям не ограничиваются планиметрией. На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат рабро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна 2а). Отсюда имеем
Возможности применения теоремы Пифагора к вычислениям не ограничиваются планиметрией. На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат рабро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна 2а). Отсюда имеем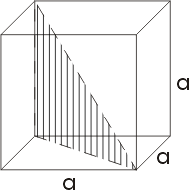 Исследуем пирамиду, например, такую, в основании которой лежит квадрат и высота которой проходит через центр этого квадрата (правильную пирамиду). Пусть сторона квадрата - а, и высота пирамиды - h. Найдем s (длину боковых ребер пирамиды).
Исследуем пирамиду, например, такую, в основании которой лежит квадрат и высота которой проходит через центр этого квадрата (правильную пирамиду). Пусть сторона квадрата - а, и высота пирамиды - h. Найдем s (длину боковых ребер пирамиды).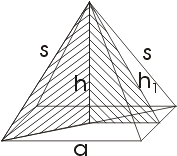 Считать эти приложения теоремы Пифагора только теоретическими - большая ошибка. Если, например, рассматривать нашу четырехугольную пирамиду как крышу башни,
Считать эти приложения теоремы Пифагора только теоретическими - большая ошибка. Если, например, рассматривать нашу четырехугольную пирамиду как крышу башни,  то в первом нашем вопросе речь идет о том, какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана предписанная высота крыши, а вопрос о величине боковой поверхности должен интересовать, например, кровельщика при подсчете стоимости кровельных работ. Заметим, что расчет площади кровли можно заметно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит: "Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила ??? на перекрываемую площадь."
то в первом нашем вопросе речь идет о том, какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана предписанная высота крыши, а вопрос о величине боковой поверхности должен интересовать, например, кровельщика при подсчете стоимости кровельных работ. Заметим, что расчет площади кровли можно заметно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит: "Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила ??? на перекрываемую площадь."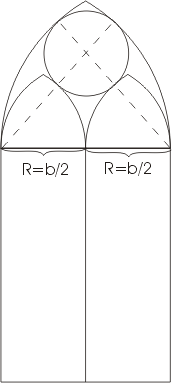 Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоватися вычисления; покажем, как применяется в таких задачах теорема Пифагора.
Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоватися вычисления; покажем, как применяется в таких задачах теорема Пифагора.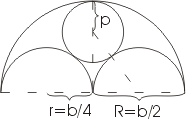
 У египтян была известна задача о лотосе. "На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну."
У египтян была известна задача о лотосе. "На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну."  Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора.
Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора.

 <!--[endif]-->
<!--[endif]-->












 Линейный вид
Линейный вид

